📌프로그래머스 인공지능 데브코스 6기 강화학습 스터디
Open AI spinning up - Introduction to RL
Key Concepts and Terminology
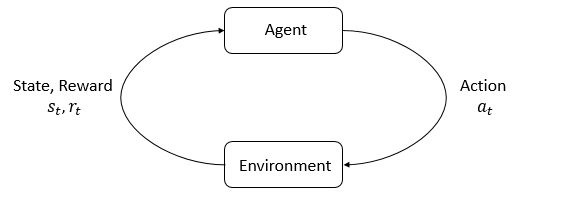
에이전트-환경 상호작용 루프
강화학습은 에이전트(agent)가 주어진 환경(environment)에서 어떻게 시행착오(trial and error)를 통해 학습하는지에 대한 연구이다. 환경은 에이전트가 살고 상호작용하는 세계이다. 에이전트는 환경으로부터 리워드(reward)를 받는다. 리워드란 현재의 상태가 얼마나 좋고 나쁜지를 알려주는 척도이다. 에이전트의 목표는 누적 리워드 리턴(return)을 최대화하는 것이다.
강화학습은 이 목표를 달성할 수 있는 행동을 배우는 방법이다.
Terminology
States and Observations
- state s : world에 대한 complete description
- observation o : state에 대한 부분적인 description
→ deep RL에서는 state와 observations를 벡터, 행렬, 고차텐서로 나타낸다.
에이전트는 세계에 대한 부분적인 정보를 가지고 행동을 결정하기 때문에 observation를 쓰는 게 더 정확한 상황에서도 일반적으로 state라고 많이 쓴다. 따라서 여기서도 standard convention을 따라 s라고 쓰도록 하겠다.
Action Spaces
다른 환경들은 각자 다른 종류의 가능한 action이 있다. 주어진 환경에서 가능한 action들의 집합을 action space라고 한다.
- discrete action spaces: Atrai, 바둑과 같이 한정된 action이 가능한 경우
- continuous action spaces: 물리적 세계의 로봇을 조종하는 것과 같이 action을 실수 벡터로 표현할 수 있는 경우
Policies
에이전트가 action을 결정하는 rule을 policy라고 한다. policy는 보상을 최대화하고자 한다. policy는 아래 식들처럼 현재 state를 넣으면 취할 action이 나오는 함수이다.
- deterministic policy
- 각 state가 하나의 action으로 매핑되어있다.
- stochastic policy
- 각 state가 action에 대한 확률분포에 매핑되어있다. 따라서 state가 주어지면 action은 확률 분포에 기반하여 랜덤하게 선택된다.
- action sampling, log-likelihood 계산의 computation 수행
- 종류
1) categorical policies: discrete action space에서 사용
2) diagonal Gaussian policies: continuous action space에서 사용
- 각 state가 action에 대한 확률분포에 매핑되어있다. 따라서 state가 주어지면 action은 확률 분포에 기반하여 랜덤하게 선택된다.
이러한 policy는 우리가 최적화 알고리즘을 쓸 수 있도록 parameterized되어있고, 계산 가능한 함수로 다뤄진다.
Trajectories
에이전트가 거친 모든 state와 action의 궤적으로, episode, rollout이라고 불리기도 한다.
$s_0$은 start-state distribution $\rho_0$에 의해 무작위로 샘플링된다.
t에서의 상태 $s_t$에서 t+1의 상태 $s_t+1$로의 state transition은 환경과 가장 최근의 action $a_t$에 의해 결정되며 결정적이거나 확률적으로 결정된다.
)
이 때 에이전트의 action은 policy에 의해 결정된다.
Reward and Return
리워드함수 R은 현재 state, 방금 한 action, 다음 state에 의존한다.
에이전트의 목적은 trajectory를 따른 누적 리워드 return을 최대화하는 것이다. return은 두 가지로 나누어진다.
1) finite-horizon undiscounted return
- 특정 기간동안 단순한 리워드의 합
2) infinite-horizon discounted return
- 모든 기간동안의 리워드의 discounted된 합(discount factor와의 가중합)
- discount의 의미는 1) 수렴을 위해 2) 현재의 가치에 더 가중치를 두기 위해
The RL Problem
강화학습의 목적은 expected return을 최대화하는 policy를 찾는 것이다.
환경 전이와 policy가 모두 확률적(stochastic)한 상황이라고 가정했을 때, T-step trajectory의 확률은 다음과 같이 나타낼 수 있다.
이 때의 expected return 함수는 다음과 같이 리워드의 기댓값으로 나타낼 수 있다.
이 때 강화학습의 중심 최적화 문제(centralized optimization problem)는 다음과 같이 표현할 수 있다.
(expected return을 최대화하는 policy를 찾는 것)
이 때의 $\pi^*$를 optimal policy라고 한다.
Value Function
현재 state, 또는 state-action pair에서 시작하여 특정 policy를 따라 이동했을 때의 예상되는 가치.(expected return)
On-policy Value Function
On-Policy Action-Value Function
Optimal Value Function
Optimal Action-Value Function
The Optimal Q-Function and the Optimal Action
optimal action-value function $Q^*(s,a)$은 state s에서 시작해서 임의의 행동 a를 하고 나서 optimal policy를 따랐을 때의 expected return을 알려준다. 따라서 $Q^*$를 알면 다음과 같이 optimal action $a^*(s)$를 구할 수 있다.
Bellman Equations
위의 네가지 value function은 벨만 방정식을 따른다. 벨만 방정식의 기본 아이디어는 “시작점의 value는 현재 state에서의 리워드와 다음 state에서의 value를 합한 것과 같다”는 것이다.
($s'$는 다음 state)
→ 위에서의 value function을 현재 상태의 리워드 + 다음 상태에서의 value로 나눈 것!
벨만 방정식과 on-policy value function, optimal value function과의 중요한 차이점은 action에 대한 $max$의 존재 여부이다. 이것이 있다는 건 agent가 action을 선택해야 할 때 optimal하게 선택하기 위해서 가장 높은 value로 이끄는 action을 선택하는 것이다.
* Bellman backup: 벨만 방정식의 우항, 현재 리워드 + 다음 value
Advantage Functions
강화학습에서는 어떤 action이 절대적으로 얼마나 좋은지보다, 다른 action들에 비해 상대적으로 얼마나 좋은지가 중요할 때가 있다. advantage function은 state s에서 policy $\pi$를 따라 특정 action a를 했을 때 $\pi(*|s)$를 따라 랜덤한 action을 했을 때 얼마나 나은지를 보여준다.
Formalism
Markov Decision Processes(MDP)
MDP는 시스템이 Markov property를 따른다는 것을 뜻한다. 마르코프 속성은 transition이 이전이 아닌, 가장 최근의 state와 action에만 의존한다는 것이다. MDP는 $<S, A, R, P, \rho_0>$라는 5-튜플로 표현된다.
$S$: 가능한 모든 state의 집합
$A$: 가능한 모든 action의 집합
$R$: 리워드 함수
$P$: transition probability function
$\rho_0$: starting state distribution
source
Open AI spinning up - Introduction to RL
https://www.baeldung.com/cs/rl-deterministic-vs-stochastic-policies